
Python을 이용한 포트폴리오 최적화: 효율적 프론티어와 자본배분선 (feat. 코스피는 신이야)
계란을 한 바구니에 담지 마라. - 제임스 토빈, 노벨경제학상 수상자
포트폴리오 최적화는 투자자의 목표 수익률과 위험 선호도에 따라 가장 적합한 자산 배분을 찾는 과정을 말합니다.
여기서 포트폴리오는 투자자가 보유한 주식과 채권 같은 여러 투자자산으로 이루어진 그룹을 뜻합니다.
현대 포트폴리오 이론(MPT; Modern Portfolio Theory)
현대 포트폴리오 이론은 위험은 낮고 기대수익률은 높은 포트폴리오가 이상적인 포트폴리오라는 상식적인 가정에서 출발합니다.
그런데 일반적으로는 High Risk, High Return란 말처럼,
높은 수익을 얻고 싶다면 높은 위험을 감수해야 하고, 낮은 위험을 원한다면 낮은 수익밖에 얻지 못합니다.
하지만 그중에서도 위험 대비 기대수익률이 높은 조합은 있을 것이고,
이것을 수학적 최적화를 통해 찾아낼 수 있다는 것이 현대 포트폴리오 이론입니다.
포트폴리오 이론의 중요한 함의는 분산 투자로,
이론의 창시자 해리 마코위츠는 상관관계가 낮은 여러 자산을 섞어서 분산 투자하게 되면 동일한 수익률을 유지하면서도 위험만 줄이는 것이 가능하다는 것을 발표하며 1990년 노벨 경제학상을 수상했습니다.
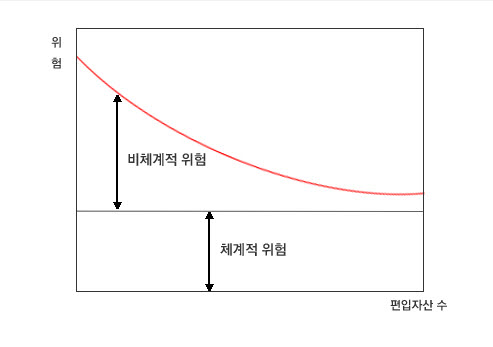
적절히 분산된 포트폴리오는 개별 투자상품의 리스크(비체계적 위험)는 0에 수렴하고 오직 시장 위험(체계적 위험)만 남으며 위험이 최소가 됩니다.
포트폴리오 최적화 실습
패키지 설치
pip install PyPortfolioOpt
PyPortfolioOpt는 포트폴리오 최적화 함수를 제공하는 라이브러리입니다.
참고: PyPortfolioOpt
pip install yfinance
yfinance는 Yahoo finance에서 주가 데이터를 가져오기 위해 사용하는 라이브러리입니다.
주가 데이터 가져오기
실습을 위해 가져올 종목은 인하대학교 Bluechip Mutual Fund의 세미나 종목으로 선정했습니다.
import yfinance as yf
ticker_names = {
'^KS11': 'KOSPI',
'^KQ11': 'KOSDAQ',
'348210.KQ': '넥스틴',
'058610.KQ': '에스피지',
'114840.KQ': '아이패밀리에스씨',
'007660.KS': '이수페타시스',
'272210.KS': '한화시스템',
'093320.KQ': '케이아이엔엑스',
'003230.KS': '삼양식품',
'024110.KS': '기업은행',
'347890.KQ': '엠투아이',
'119610.KQ': '인터로조',
'215000.KQ': '골프존',
'336260.KS': '두산퓨얼셀',
'005300.KS': '롯데칠성',
'281740.KQ': '레이크머티리얼즈',
'253450.KQ': '스튜디오드래곤',
'213420.KQ': '덕산네오룩스',
'006890.KS': '태경케미컬',
'060720.KQ': 'KH바텍',
'190510.KQ': '나무가',
'002310.KS': '아세아제지',
'013310.KQ': '아진산업',
'003720.KS': '삼영',
'025320.KQ': '시노펙스',
'383310.KQ': '에코프로에이치엔',
'145720.KS': '덴티움',
'337930.KQ': '브랜드엑스코퍼레이션',
'393890.KQ': '더블유씨피',
'074600.KQ': '원익QnC',
'251970.KQ': '펌텍코리아',
'166090.KQ': '하나머티리얼즈',
'036890.KQ': '진성티이씨',
'089850.KQ': '유비벨록스',
'403870.KQ': 'HPSP',
'104540.KQ': '코렌텍',
'047810.KS': '한국항공우주',
'183300.KQ': '코미코',
'298050.KS': '효성첨단소재',
'214150.KQ': '클래시스',
'086670.KQ': '비엠티',
'078350.KQ': '한양디지텍',
'307950.KS': '현대오토에버',
'332370.KQ': '아이디피',
'192820.KS': '코스맥스',
'259960.KS': '크래프톤',
}
tickers = list(ticker_names.keys())
df = yf.download(tickers)
prices = df["Adj Close"].dropna(how="all")
prices.rename(columns=ticker_names, inplace=True)
[*********************100%%**********************] 46 of 46 completed
자본 자산 가격결정 모형(CAPM; Capital Asset Pricing Model)
개별 종목의 기대수익률은 시장 전체 수익률의 흐름에 영향을 받는다.
CAPM은 기업의 가치를 계산하거나 자산에 대한 투자 결정을 보조할 때 가장 많이 사용되는 재무 모델로,
해리 마코위츠가 창안한 현대 포트폴리오 이론을 기반으로 하는 재무가치 평가 모델입니다.
\[R_i=R_f+\beta_i(E(R_m)-R_f)\]- \(R_i\): 위험자산의 기대수익률
- \(R_f\): 무위험자산의 수익률
- \(R_m\): 시장 수익률
- \(\beta_i\): 베타(위험자산의 민감도)
여기서 베타는 특정 자산의 체계적 위험을 측정해주는 지표입니다.
\[\beta_i=\frac{Cov(R_i,R_m)}{Var(R_m)}\]\(\beta_i\)는 선형 회귀식을 통해서 유도할 수 있습니다.
CAPM에서는 각 자산의 초과수익률을 아래와 같이 표현합니다. (위의 CAPM 식에서 \(R_f\)를 단순히 좌변으로 이동)
\[R_i-R_f=\beta_i(E(R_m)-R_f)\]위 식은 아래와 같은 형태로 나타낼 수 있습니다. (\(y_t=R_i-R_f\), \(x_t=E(R_m)-R_f\))
\[\hat{y_t}=\beta_i x_t\] \[\hat{e_t}=y_t-\beta_i x_t\]최소 제곱 원칙(Least Squares Principle)을 통해 \(\beta_i\)를 추정합니다.
\[SSE=\min{\sum{\hat{e_t}^2}}=\min{\sum{(y_t-\beta_i x_t)^2}}\] \[\frac{\partial\sum{(y_t-\beta_i x_t)^2}}{\partial\beta_i}=\frac{\partial(\sum{y_t^2-2\beta_i\sum{x_t y_t}+\beta_i^2\sum{x_t^2}})}{\partial\beta_i}=-2\sum{x_t y_t}+2\beta_i\sum{x_t^2}=0\] \[\beta_i=\frac{\sum{x_t y_t}}{\sum{x_t^2}}\]여기서, 분자와 분모를 \(n\)으로 나눠줍니다.
\[\beta_i=\frac{\frac{\sum{x_t y_t}}{n}}{\frac{\sum{x_t^2}}{n}}\]\(x_t\)와 \(y_t\)는 각각 시장과 자산의 초과수익률을 의미하므로, CAPM에서 \(E(x_t)=E(y_t)=0\)입니다.
\[Cov(R_i,R_m)=\frac{\sum{(x_t-E(x_t))(y_t-E(y_t))}}{n}=\frac{\sum{x_t y_t}}{n}\] \[Var(R_m)=\frac{\sum{(x_t-E(x_t))^2}}{n}=\frac{\sum{x_t^2}}{n}\] \[\beta_i=\frac{\frac{\sum{x_t y_t}}{n}}{\frac{\sum{x_t^2}}{n}}=\frac{Cov(R_i,R_m)}{Var(R_m)}\]
CAPM에서는 개별 종목의 기대수익률은 개별 종목의 위험에 비례하며,
따라서 과거의 베타를 통해 개별 종목의 기대수익률을 추정할 수 있다고 주장합니다.
from pypfopt import expected_returns
risk_free_rate = 0.035
mu = expected_returns.capm_return(prices, market_prices=prices['KOSPI'].to_frame(), risk_free_rate=risk_free_rate, frequency=252)
mu.plot.barh(figsize=(5, 10))
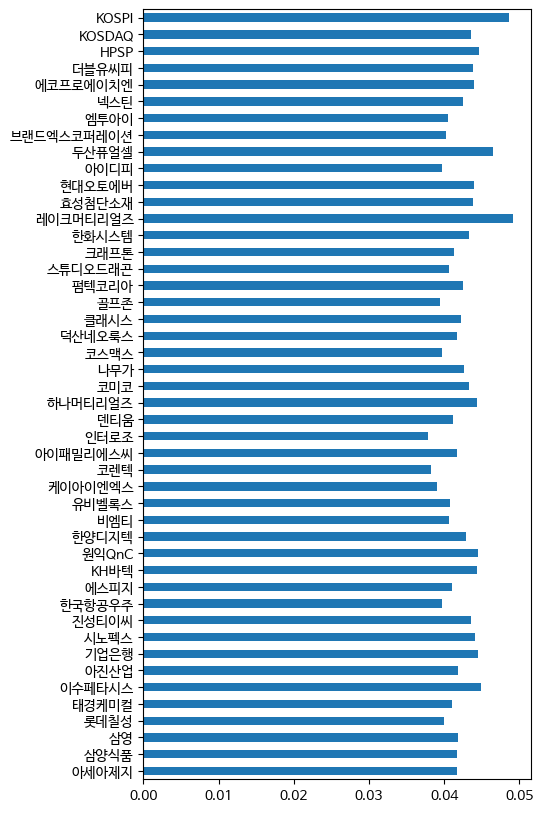
무위험자산의 수익률은 한국무위험지표금리(KOFR)의 1년 평균을 사용해 3.5%로 잡았고,
베타와 기대수익률 계산에서의 참고할 시계열 길이는 1년으로 정의했습니다.
1년 중 주식거래가 가능한 날(평일)이 약 252일이기 때문에
frequency=252는 1년 치 주가를 의미합니다.
표본 공분산
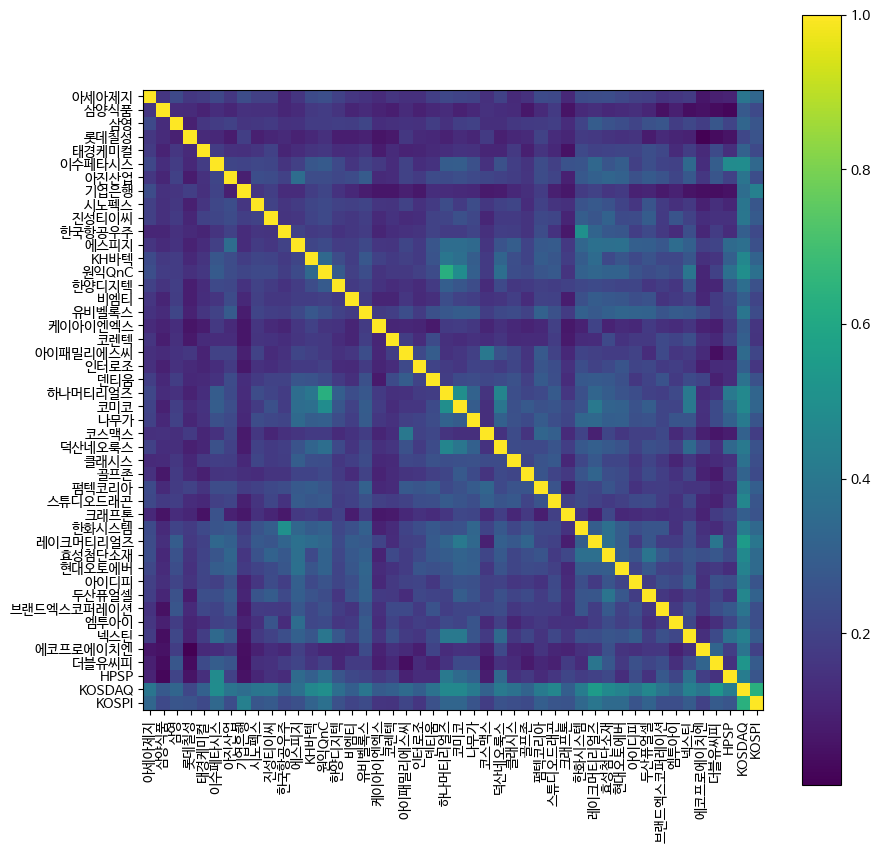
다음은 각 자산간 상관관계(Correlation)를 구해야 합니다.
\[\rho_{X,Y}=Corr(X,Y)=\frac{Cov(X,Y)}{\sigma_X \sigma_Y}\]상관관계는 공분산을 통해서 계산할 수 있습니다.
import matplotlib.pyplot as plt
import numpy as np
from pypfopt import risk_models
from pypfopt import plotting
S = risk_models.sample_cov(prices, frequency=252)
# Plot the correlation matrix
matrix = risk_models.cov_to_corr(S)
fig, ax = plt.subplots(figsize=(10, 10))
cax = ax.imshow(matrix)
fig.colorbar(cax)
ax.set_xticks(np.arange(0, matrix.shape[0], 1))
ax.set_xticklabels(matrix.index)
ax.set_yticks(np.arange(0, matrix.shape[0], 1))
ax.set_yticklabels(matrix.index)
plt.xticks(rotation=90)
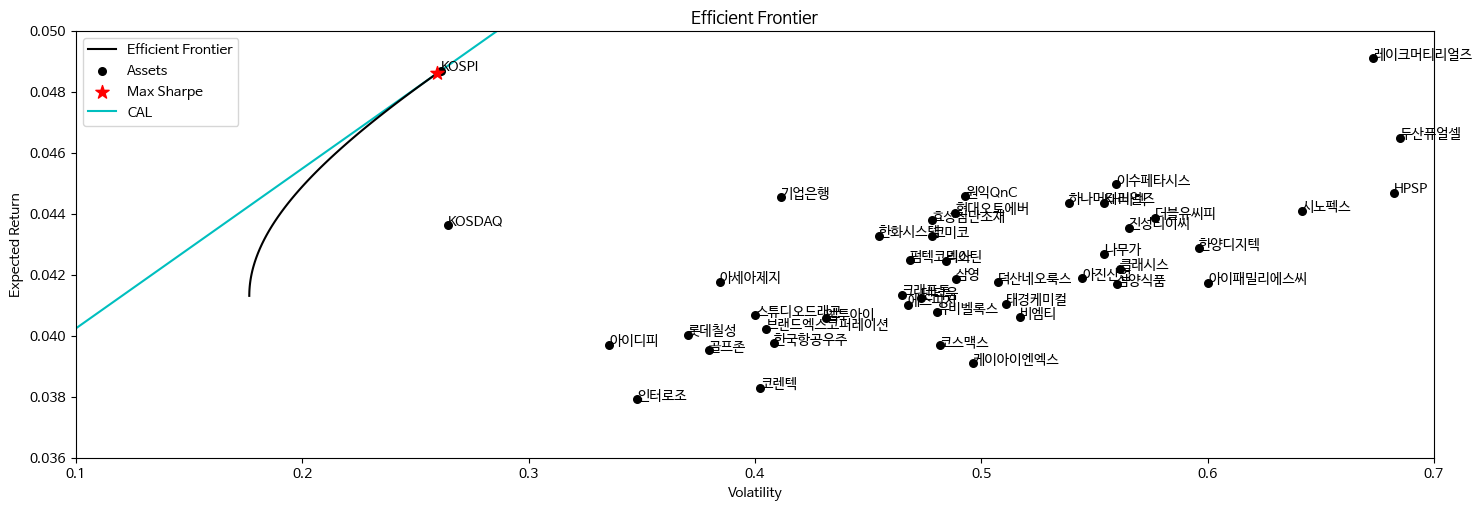
효율적 프론티어(Efficient Frontier)
투자 대상 중 가장 적절한 수익률과 위험(변동성)을 가진 종목을 이은 곡선
주어진 위험 수준에 비춰 가장 높은 수익률을 제공하는 포트폴리오를 효율적 포트폴리오라고 부릅니다.
현대 포트폴리오 이론에서 위험은 수익률의 변동성으로 정의됩니다.
여기서 변동성은 과거 수익률의 표준편차를 말합니다.
자산의 수익률이 평균으로부터 많이 움직일수록, 얻게 되는 수익률의 범위가 커지기 때문에 위험이 크다고 할 수 있습니다.
효율적 프론티어는 동일한 기대 수익률 내에서 가장 작은 위험을 가진 포트폴리오의 집합입니다.
일반적으로 개별 종목의 기대수익률은 개별 종목의 위험에 비례하며 커지는데,
그 중에서도, 특히나 기대수익률 대비 위험이 큰 종목도 있고 낮은 종목도 있기 마련입니다.
효율적 프론티어란 동일한 위험에서 가장 높은 수익률을 기대할 수 있는 종목들을 선으로 이은 것이라고 생각하면 됩니다.
import matplotlib.pyplot as plt
from pypfopt import plotting
from pypfopt.efficient_frontier import EfficientFrontier
fig, ax = plt.subplots(figsize=(15, 5))
ef = EfficientFrontier(mu, S)
for name in list(ticker_names.values()):
if name != 'KOSPI' and name != 'KOSDAQ':
ef.add_constraint(lambda w: w[ef.tickers.index(name)] <= 0.1) # 개별종목 비중 10% 안 넘게
# Plot efficient frontier
plotting.plot_efficient_frontier(ef.deepcopy(), ax=ax, show_tickers=True)
ax.get_lines()[0].set_color("black")
# Plot the tangency portfolio
ef.max_sharpe(risk_free_rate)
weights = ef.clean_weights()
ret_tangent, std_tangent, _ = ef.portfolio_performance(verbose=True, risk_free_rate=risk_free_rate)
ax.scatter(std_tangent, ret_tangent, s=100, c="r", marker="*", label="Max Sharpe", zorder=10)
# Plot capital allocation line
ax.plot([0, std_tangent, std_tangent*2], [risk_free_rate, ret_tangent, 2*ret_tangent-risk_free_rate], 'c', label='CAL', zorder=-1)
# Format
ax.set_title("Efficient Frontier")
ax.set_ylabel('Expected Return')
ax.set_xlim(0.1, 0.7)
ax.set_ylim(0.036, 0.05)
handles, labels = ax.get_legend_handles_labels()
labels[0], labels[1] = ['Efficient Frontier', 'Assets']
ax.legend(handles, labels)
plt.show()
Expected annual return: 4.9%
Annual volatility: 26.0%
Sharpe Ratio: 0.05
일반적으로 포트폴리오에서는 단일 종목의 비중이 너무 크지 않게 제약을 걸곤 합니다.
여기서는 개별종목 비중 제한을 10%로 설정했습니다.
효율적 프론티어 우측 끝 단에 코스피 지수가 위치합니다.
코스닥은 코스피보다 위험은 크고 기대 수익률은 낮은 결과를 보였습니다.
fig, ax = plt.subplots(figsize=(5, 10))
plotting.plot_weights(weights, ax=ax)

효율적 포트폴리오를 보면 개별주는 최대한 건들지 말고 포트폴리오에 코스피를 98% 이상 담으라는 결과가 나옵니다.
실습 결과 해석
자본배분선(CAL; Capital Allocation Line)
실습 결과에서 검정색 효율적 프론티어 곡선을 접하는 청색 직선은 자본배분선이라 부릅니다.
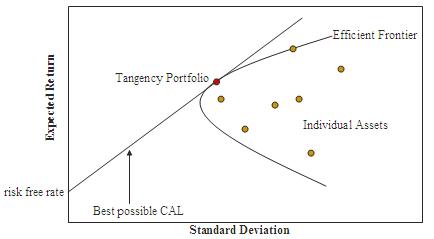
현대 포트폴리오 이론에서 도출된 위험자산만으로 구성된 효율적 포트폴리오에 무위험자산을 포함시키면,
더 낮은 위험과 높은 기대수익률을 갖는 새로운 포트폴리오 집합이 나오는데, 이를 자본배분선이라 합니다.
자본배분선의 y 절편은 무위험자산을 100% 보유하는 포트폴리오이므로 기대 수익률은 무위험수익률과 동일합니다.
자본배분선과 효율적 프론티어 곡선이 접하는 지점은 위험자산만을 보유했을 때 가장 효율적인 포트폴리오를 나타냅니다.
샤프 비율(Sharpe Ratio)
샤프 비율은 해리 마코위츠의 제자 윌리엄 샤프가 개발한 투자 성과 판단용 지표로,
총위험(total risk)에 집중하는 위험 대 보상 비율(Reward-to-risk Ratio)입니다.
\[Sharpe=\frac{R_p-R_f}{\sigma_p}\]높은 샤프 비율을 기록하는 투자일수록 더 적은 위험으로 더 높은 수익률을 내는 것이라고 볼 수 있습니다.
샤프 비율이 0 이하라면 시장수익률보다 낮은 수익률을 기록하는 것이기 때문에,
샤프 비율이 0 이상이어야 투자의 고려 대상이 될 수 있고,
1 이상이면 상당히 괜찮은 투자라고 볼 수 있습니다.
자본배분선과 효율적 프론티어 곡선이 접하는 지점이 샤프 비율이 최대가 되는 포트폴리오입니다.
효율적 시장 가설(EMH; Efficient Market Hypothesis)
효율적 시장 가설은 가격은 상품에 대해 얻을 수 있는 모든 정보를 빠르게 반영하기 때문에,
투자자는 장기적으로 시장 수익률을 넘을 수 없다는 가설입니다.
앞서 개별주와 시장 지수(Market Index)를 포함하는 포트폴리오를 최적화했는데,
코스피가 효율적 프론티어 위에 위치했음은 물론,
포트폴리오에 코스피를 98% 이상 담으라는 결과가 나왔습니다.
이는 코스피 100%를 보유하는 것도 매우 효율적인 포트폴리오라는 말이고,
2%의 개별주를 넣으라는 것은 오히려 단기적인 오차로 인한 결과로 의심됩니다.
즉, 한국의 주식 시장은 효율적 시장 가설을 잘 따라간다고 볼 수 있습니다.
올해 코스피 지수가 전년 대비 많이 올랐는데 개별주로는 큰돈을 벌기 어려웠던 이유도,
코스피 자체가 매우 효율적인 포트폴리오이기 때문이라고 추측할 수 있습니다.
결론
- 코스피는 신이다.
- 확실한 정보가 없다면 개별주는 건들지 말자.
- 코스닥은 코스피의 하위호환 포트폴리오지만, 분산투자 효과로 인해 대부분의 개별주보다는 나은 선택이다.