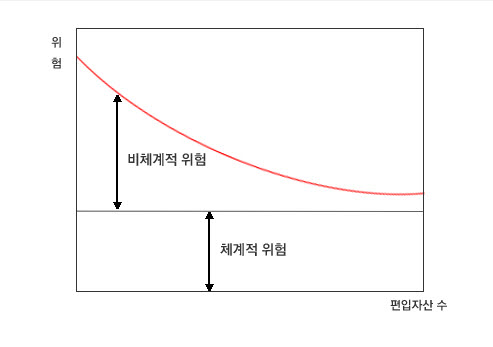
주저하는 투자자를 위해: Python으로 구현하는 최소-분산 포트폴리오
투자에서 수익률은 투자자의 중요한 목표 중 하나입니다.
하지만, 수익률이 높을수록 위험이 높아지는 것은 시장의 기본 원칙이죠.
따라서 투자자는 수익률과 위험의 조화를 이루는 포트폴리오를 구성해야 합니다.
자산배분 모형에 대한 연구는 해리 마코위츠가 제안한 평균-분산 모형에서 시작됩니다.
평균-분산 모형
평균-분산 모형은 개별 투자 종목의 기대수익률과 위험을 평균(\(\mu\))과 분산(\(\sigma^2\))으로 정의하는 계량 모형입니다.
마코위츠는 분산투자의 수학적 방식인 최적화 함수를 제시함으로써 현대 포트폴리오 이론의 중요한 근간을 제공하고, 그 공로로 1991년 노벨 경제학상을 받았습니다.
최적화 함수로부터 생성되는 최적 포트폴리오는 대표적으로 최소-분산 포트폴리오 와 접선 포트폴리오 가 있습니다.
최소-분산 포트폴리오는 위험을 최소화하는 포트폴리오의 한 종류로,
포트폴리오의 분산을 최소화하는 투자 비중을 찾는 방법으로 구성됩니다.
반면, 접선 포트폴리오는 샤프 지수(투자 성과)가 최대가 되도록 구성 종목의 투자 비중을 결정합니다.
최소-분산 포트폴리오를 찾기 위해서는 먼저 포트폴리오의 기대수익률과 위험을 수학적으로 정의해야 합니다.
포트폴리오의 기대수익률
가중치만큼 각 종목의 기대수익률을 더하면 됩니다.
\[\mu_p=E(R_p)=w_1 E(R_1)+w_2 E(R_2)\]이때, \(w_1+w_2=1\)
일반화(n개의 종목)
\[\mu_p=E(R_p)=\sum{w_i E(R_i)}\]이때, \(\sum{w_i}=1\)
포트폴리오 수익률의 분산
포트폴리오 수익률의 분산은 포트폴리오의 수익률 변동의 정도를 나타내는 지표로, 분산이 클수록 위험이 크다고 볼 수 있다.
먼저, 분산의 정의를 이용합니다.
\[\sigma_p^2=E[R_p-E(R_p)]^2\]식을 전개합니다.
\[\sigma_p^2=E[w_1 R_1+w_2 R_2-(w_1E(R_1)+w_2E(R_2))]^2\]\(w\)로 항을 묶어줍니다.
\[\sigma_p^2=E[w_1(R_1-E(R_1))+w_2(R_2-E(R_2))]^2\] \[=E[w_1^2(R_1-E(R_1))^2+2w_1 w_2(R_1-E(R_1))(R_2-E(R_2))+w_2^2(R_2-E(R_2))^2]\] \[=w_1^2 E[R_1-E(R_1)]^2+2w_1 w_2 E[(R_1-E(R_1))(R_2-E(R_2))]+w_2^2 E[R_2-E(R_2)]^2\] \[=w_1^2\sigma_1^2+2w_1 w_2\mathrm{Cov}(R_1,R_2)+w_2^2\sigma_2^2\]공분산 \(\mathrm{Cov}(R_1,R_2)=\sigma_1\sigma_2\rho_{12}\)이므로,
\[\sigma_p^2=w_1^2\sigma_1^2+2w_1 w_2\sigma_1\sigma_2\rho_{12}+w_2^2\sigma_2^2\quad\cdots(1)\]일반화(n개의 종목)
\[\sigma_p^2=E[R_p-E(R_p)]^2\] \[=E[\sum{w_i R_i}-\sum{w_i E(R_i)}]^2\]\(w\)로 항을 묶어줍니다.
\[\sigma_p^2=E[\sum{w_i(R_i-E(R_i))}]^2\] \[=E[\sum{w_i^2(R_i-E(R_i))^2}+\sum\sum_{i\neq{j}}{w_i w_j(R_i-E(R_i))(R_j-E(R_j))}]\]\(E[\quad]\)를 \(\sum\) 안으로 넣어줍니다.
\[\sigma_p^2=\sum{w_i^2 E[R_i-E(R_i)]^2}+\sum\sum_{i\neq{j}}{w_i w_j E[(R_i-E(R_i))(R_j-E(R_j))]}\] \[=\sum{w_i^2 \sigma_i^2}+\sum\sum_{i\neq{j}}{w_i w_j\mathrm{Cov}(R_i,R_j)}\] \[=\sum{w_i^2 \sigma_i^2}+\sum\sum_{i\neq{j}}{w_i w_j\sigma_1\sigma_2\rho_{12}}\quad\cdots(2)\] \[=\sum\sum{w_i w_j\sigma_1\sigma_2\rho_{12}}\] \[=\sum\sum{w_i w_j\mathrm{Cov}(R_i,R_j)}\]여기서 그냥 전개하면 식이 길어지니, 행렬로 풀어봅시다.
공분산 행렬은 아래와 같이 정의됩니다.
\[\mathbf{\Sigma}=\mathrm{Cov}(X,X)=E[(X-E(X))(X-E(X))^\mathsf{T}]\]여기서 \(\mathbf{\Sigma}\)(시그마)는 합 연산이 아니라 공분산 행렬을 나타내는 기호입니다.
\(\sigma_p^2\)를 행렬 표현으로 변환합니다.
\[\sigma_p^2=\sum\sum{w_i w_j\mathrm{Cov}(R_i,R_j)}=\mathbf{w}^\mathsf{T}\mathbf{\Sigma w}\quad\cdots(3)\](TMI) 분산투자의 효과
마코위츠는 이전까지 추상적으로만 존재하던 분산투자의 효율성을 수학적으로 증명했습니다.
앞서 저희는 (2)식에서 \(\sigma_p^2\)는 아래와 같이 표현된다고 정리했습니다.
\[\sigma_p^2=\sum{w_i^2 \sigma_i^2}+\sum\sum_{i\neq{j}}{w_i w_j\sigma_i\sigma_j\rho_{ij}}\]만약 포트폴리오가 동일 가중이면 \(w_i=\frac{1}{n}\)입니다.
따라서 \(\sigma_p^2\)는,
\[\sigma_p^2=\sum{\frac{\sigma_i^2}{n^2}}+\sum\sum_{i\neq{j}}{\frac{\sigma_i\sigma_j\rho_{ij}}{n^2}}=\frac{1}{n}\sum{\frac{\sigma_i^2}{n}}+\frac{n-1}{n}\sum\sum_{i\neq{j}}{\frac{\sigma_i\sigma_j\rho_{ij}}{n(n-1)}}\] \[=\frac{1}{n}\overline{\sigma_i^2}+\frac{n-1}{n}\overline{\sigma_i\sigma_j\rho_{ij}}\]포트폴리오에 종목을 계속 추가한다면,
즉, \(n\)이 무한대로 간다면,
\[\lim_{n\to\infty}{\sigma_p^2}=\lim_{n\to\infty}{(\frac{1}{n}\overline{\sigma_i^2}+\frac{n-1}{n}\overline{\sigma_i\sigma_j\rho_{ij}})}=\overline{\sigma_i\sigma_j\rho_{ij}}\]개별 종목의 분산의 합은 0에 수렴하게 되지만, 일정 수준 밑으로는 내려가지 않는 것을 확인할 수 있습니다.
또한, 종목 간의 상관관계(\(\rho_{ij}\))가 낮을수록 포트폴리오 전체의 분산(\(\sigma_p^2\))이 작아지는 것을 알 수 있습니다.
최소-분산 최적화(Minimum Variance Optimization)
포트폴리오의 분산 \(\sigma_p^2\)가 최소로 만들기 위해서는, \(\sigma_p\)를 최소로 만들어야 합니다.
(1)식을 가져와서 \(\sigma_p\)을 구합니다.
\[\sigma_p=\sqrt{w_1^2\sigma_1^2+2w_1 w_2\sigma_1\sigma_2\rho_{12}+w_2^2\sigma_2^2}\]\(w_1+w_2=1\)이므로,
\[\sigma_p=\sqrt{w_1^2\sigma_1^2+2w_1(1-w_1)\sigma_1\sigma_2\rho_{12}+(1-w_1)^2\sigma_2^2}\]\(w_1\)로 미분해 기울기가 0이 되는(\(\sigma_p\)가 최소가 되는) 지점을 찾아줍니다.
\[\frac{\partial \sigma_p}{\partial w_1}=\frac{2w_1\sigma_1^2+2(1-2w_1)\sigma_1\sigma_2\rho_{12}-2(1-w_1)\sigma_2^2}{2\sqrt{w_1^2\sigma_1^2+2w_1(1-w_1)\sigma_1\sigma_2\rho_{12}+(1-w_1)^2\sigma_2^2}}=0\] \[w_1\sigma_1^2+(1-2w_1)\sigma_1\sigma_2\rho_{12}-(1-w_1)\sigma_2^2=0\] \[w_1\sigma_1^2-2w_1\sigma_1\sigma_2\rho_{12}+w_1\sigma_2^2=\sigma_2^2-\sigma_1\sigma_2\rho_{12}\] \[w_1=\frac{\sigma_2^2-\sigma_1\sigma_2\rho_{12}}{\sigma_1^2-2\sigma_1\sigma_2\rho_{12}+\sigma_2^2}\quad\cdots(4)\]따라서 포트폴리오에 종목 1을 \(w_1\)만큼, 종목 2을 \((1-w_1)\)만큼 담으면 포트폴리오 수익률의 분산이 최소가 됩니다.
실습
삼성전자, 현대차, NAVER, POSCO홀딩스, LG화학 다섯 개 종목의 주가 기록을 다운로드 합니다.
import yfinance as yf
tickers = ['005930.KS', '005380.KS', '035420.KS', '005490.KS', '051910.KS']
df = yf.download(tickers)
prices = df["Adj Close"].dropna(how="all")
returns = prices.pct_change().dropna(how="all")
returns_5y = returns[-(252*5+1):-1]
각 종목의 최근 5년 연 평균 수익률과 종목간의 공분산을 구합니다.
여기서 수익률은 코딩을 간단히 하기 위해서 역사적 수익률을 사용했습니다.
실제 투자 포트폴리오를 최적화할 때는 CAPM 등을 이용해 구한 기대수익률을 사용하시길 바랍니다.
mu = (1 + returns_5y).prod() ** (252 / returns_5y.count()) - 1
cov = returns_5y.cov() * 252
먼저 삼성전자, 현대차 두 종목으로만 이루어진 포트폴리오를 최적화해 보겠습니다.
삼성전자, 현대차의 수익률 표준편차(\(\sigma_1\), \(\sigma_2\))와 상관계수(\(\rho_{12}\))를 구합니다.
import math
mu_1 = mu['005930.KS']
mu_2 = mu['005380.KS']
sigma_1 = math.sqrt(cov['005930.KS']['005930.KS'])
sigma_2 = math.sqrt(cov['005380.KS']['005380.KS'])
rho_12 = cov['005930.KS']['005380.KS'] / (sigma_1 * sigma_2)
(1)식을 이용해 포트폴리오의 분산을 구합니다.
\[\sigma_p^2=w_1^2\sigma_1^2+2w_1 w_2\sigma_1\sigma_2\rho_{12}+w_2^2\sigma_2^2\quad\cdots(1)\]import numpy as np
w = np.linspace(1, 0, 21)
mu_w = w*mu_1 + (1-w)*mu_2
sigma_w = np.sqrt(w**2*sigma_1**2 + 2*w*(1-w)*sigma_1*sigma_2*rho_12 + (1-w)**2*sigma_2**2)
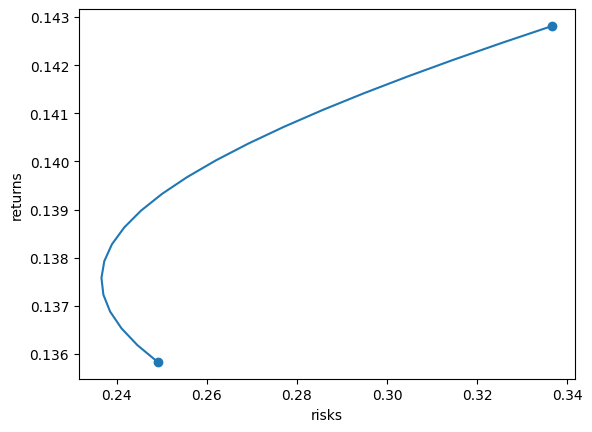
그래프로 그리면 아래와 같습니다.
import matplotlib.pyplot as plt
plt.plot(sigma_w, mu_w, zorder=-1)
plt.scatter([sigma_1, sigma_2], [mu_1, mu_2])
plt.xlabel('risks')
plt.ylabel('returns')
최소-분산 포트폴리오는 (4)식을 이용해 구합니다.
\[w_1=\frac{\sigma_2^2-\sigma_1\sigma_2\rho_{12}}{\sigma_1^2-2\sigma_1\sigma_2\rho_{12}+\sigma_2^2}\quad\cdots(4)\]w_mv = (sigma_2**2 - sigma_1*sigma_2*rho_12) / (sigma_1**2 - 2*sigma_1*sigma_2*rho_12 + sigma_2**2)
mu_mv = w_mv * mu_1 + (1-w_mv) * mu_2
sigma_mv = np.sqrt(w_mv**2*sigma_1**2 + 2*w_mv*(1-w_mv)*sigma_1*sigma_2*rho_12 + (1-w_mv)**2*sigma_2**2)
print(w_mv, 1-w_mv)
0.75478 0.24522
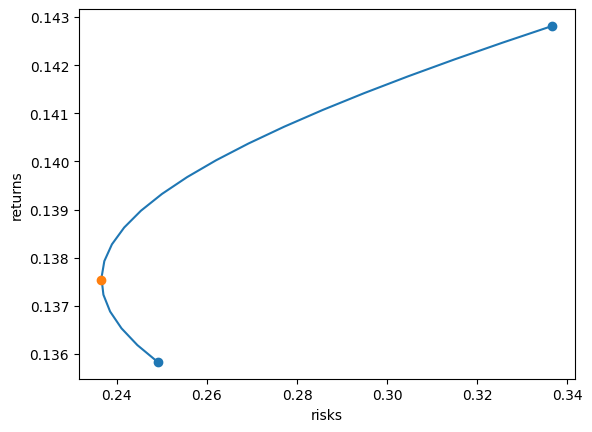
삼성전자를 75.5%, 현대차를 24.5% 담으면, 포트폴리오 수익률의 분산이 최소가 됩니다.
plt.plot(sigma_w, mu_w, zorder=-1)
plt.scatter([sigma_1, sigma_2], [mu_1, mu_2])
plt.scatter([sigma_mv], [mu_mv])
plt.xlabel('risks')
plt.ylabel('returns')
일반화(n개의 종목)
(3)식에서 일반화된 포트폴리오 수익률의 분산을 구했습니다.
\[\sigma_p^2=\mathbf{w}^\mathsf{T}\mathbf{\Sigma w}\quad\cdots(3)\]따라서, 최소-분산 포트폴리오는 분산 \(\mathbf{w}^\mathsf{T}\mathbf{\Sigma w}\)를 최소로 만드는 \(\mathbf{w}\)를 찾으면 됩니다.
\[\min_{\mathbf{w}}{\sigma_p^2}=\min_{\mathbf{w}}{\mathbf{w}^\mathsf{T}\mathbf{\Sigma w}}\]\(\mathbf{w}\)의 제약조건으로 비중의 합이 100%가 되게 합니다.
\[\text{s.t. }\sum{w_i}=1\]행렬 표현으로 바꾸면 다음과 같습니다.
\[\text{s.t. }\mathbf{w}^\mathsf{T}\mathbf{1}=1\]여기서 \(\mathbf{1}\)는 모두 1로 이루어진 벡터(=\([1,1,1,\cdots,1]^\mathsf{T}\))입니다.
수학에서 벡터와 행렬은 관행적으로 굵은 글자로 표기합니다.
라그랑주 승수법(Lagrange Multiplier Method)를 이용해 풀어줍니다.
\[L(\mathbf{w},\lambda)=\frac{1}{2}\mathbf{w}^\mathsf{T}\mathbf{\Sigma w}+\lambda(\mathbf{w}^\mathsf{T}\mathbf{1}-1)\]\(\mathbf{w}^\mathsf{T}\mathbf{\Sigma w}\) 앞에 \(\frac{1}{2}\)을 붙인 이유는 미분할 때 식을 깔끔하게 만들기 위함입니다.
\(\mathbf{\Sigma}\)는 대칭 행렬이므로,
\[\mathbf{\Sigma}=\mathbf{\Sigma}^\mathsf{T}\] \[\frac{\partial \mathbf{w}^\mathsf{T}\mathbf{\Sigma w}}{\partial \mathbf{w}}=(\mathbf{\Sigma}+\mathbf{\Sigma}^\mathsf{T})\mathbf{w}=2\mathbf{\Sigma w}\]앞에 \(\frac{1}{2}\)을 붙이게 되면,
\[\frac{\partial(\frac{1}{2}\mathbf{w}^\mathsf{T}\mathbf{\Sigma w})}{\partial \mathbf{w}}=\mathbf{\Sigma w}\]
KKT(Karush-Kuhn-Tucker) 조건을 이용해 계속 풀어줍니다.
\[\frac{\partial L}{\partial \mathbf{w}}=\mathbf{\Sigma w}+\lambda\mathbf{1}=0\] \[\mathbf{\Sigma w}=-\lambda\mathbf{1}\]양변에 \(\mathbf{\Sigma}^{-1}\)를 곱해주면,
\[\mathbf{w}=-\lambda\mathbf{\Sigma}^{-1}\mathbf{1}\quad\cdots(5)\]이제 \(\lambda\)를 구합니다.
\(\mathbf{w}^\mathsf{T}\mathbf{1}=1\)는 아래와 같이 표현할 수 있습니다.
\[\mathbf{1}^\mathsf{T}\mathbf{w}=1\](5)식과 연립하여 \(\mathbf{w}\)를 소거합니다.
\[\mathbf{1}^\mathsf{T}(-\lambda\mathbf{\Sigma}^{-1}\mathbf{1})=-\lambda\mathbf{1}^\mathsf{T}\mathbf{\Sigma}^{-1}\mathbf{1}=1\] \[-\lambda=\frac{1}{\mathbf{1}^\mathsf{T}\mathbf{\Sigma}^{-1}\mathbf{1}}\]정리하면,
\[\mathbf{w}=\frac{1}{\mathbf{1}^\mathsf{T}\mathbf{\Sigma}^{-1}\mathbf{1}}\mathbf{\Sigma}^{-1}\mathbf{1}\quad\cdots(6)\]참고: Karush-Kuhn-Tucker, KKT 카루시-쿤-터커 조건
실습(n개의 종목)
파이썬으로 (6)식을 표현하면 다음과 같습니다.
\[\mathbf{w}=\frac{1}{\mathbf{1}^\mathsf{T}\mathbf{\Sigma}^{-1}\mathbf{1}}\mathbf{\Sigma}^{-1}\mathbf{1}\quad\cdots(6)\]iota = np.ones(len(mu))
cov_inv = np.linalg.inv(cov)
w_mv5 = (cov_inv @ iota) / (iota.T @ cov_inv @ iota)
[0.14734513 0.14677826 0.50613624 0.17895709 0.02078328]
제약조건이 간단하여 \(\sum{w_i}=1\)만 맞춰주면 되기에 \(\lambda\)를 직접 계산하는 대신, 아래와 같이 \(\mathbf{w}\)를 구하는 방법도 있습니다.
w_mv5 = np.linalg.inv(cov) @ np.ones(len(mu)) w_mv5 = w_mv5 / w_mv5.sum()
삼성전자: 14.7%현대차: 14.7%NAVER: 50.6%POSCO홀딩스: 17.9%LG화학: 2.1%
최소-분산일 때의 포트폴리오 기대수익률과 분산을 구합니다.
\[\mu_p=\mathbf{w}^\mathsf{T}\mathbf{\mu}\] \[\sigma_p^2=\mathbf{w}^\mathsf{T}\mathbf{\Sigma w}\]mu_mv5 = w_mv5.T @ mu
sigma_mv5 = w_mv5.T @ cov @ w_mv5
그래프를 그립니다.
plt.plot(sigma_w, mu_w, zorder=-1)
plt.scatter(
[math.sqrt(cov['005930.KS']['005930.KS']), math.sqrt(cov['005380.KS']['005380.KS']), math.sqrt(cov['035420.KS']['035420.KS']), math.sqrt(cov['005490.KS']['005490.KS']), math.sqrt(cov['051910.KS']['051910.KS'])],
[mu['005930.KS'], mu['005380.KS'], mu['035420.KS'], mu['005490.KS'], mu['051910.KS']])
plt.scatter([sigma_mv5], [mu_mv5])
plt.xlabel('risks')
plt.ylabel('returns')
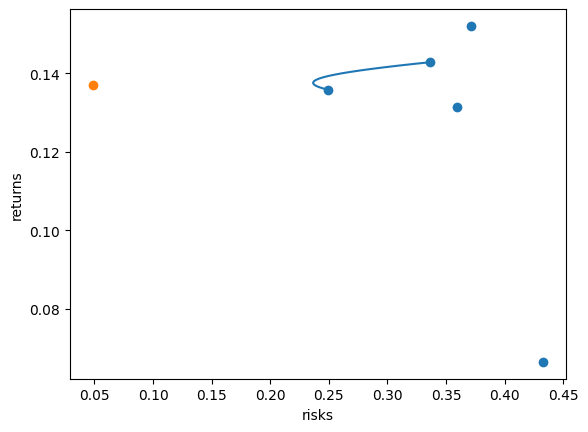
두 종목이었을 때보다 더 낮은 위험을 가진 포트폴리오가 나오는 것을 확인할 수 있습니다.
실습(n개의 종목+비중 제한)
앞서 실습에서 NAVER는 포트폴리오의 과반을 차지하고, LG화학은 비중이 2.1%로 포트폴리오에 거의 포함되지 않았습니다.
이처럼 실제 주가 데이터를 이용하여 최적 해를 계산하면,
기대수익이 높거나 음의 상관계수를 가진 일부 종목에 집중된 포트폴리오를 최적해로 제시하는 코너 해(Corner solution) 현상이 나오곤 합니다.
참고: 모서리해(Corner solution)? 내부해(Interior solution)?
이렇게 되면 분산투자를 통해 개별 종목 고유의 위험을 축소하는 분산 투자 효과가 작아지게 됩니다.
그래서 현실에서는 이런 과최적화 문제를 해결하기 위해, 개별 종목에 비중 제한을 두곤 합니다.
\[\min_{\mathbf{w}}{\mathbf{w}^\mathsf{T}\mathbf{\Sigma w}}\] \[\text{s.t. }\sum{w_i}=1\] \[w_i\geq 0.05\] \[w_i\leq 0.4\]이런식으로 가중치에 부등식으로 제약조건을 걸면, 일부 종목이 과하게 담기거나 일부 종목을 아예 포함하지 않는 현상이 완화됩니다.
하지만, 제약조건이 복잡해질수록 라그랑주 승수법으로는 문제를 해결하기 어려워집니다.
그래서 이번에서는 수치해석적 방법을 이용해 포트폴리오를 최적화해 볼 것입니다.
CVXPY
import cvxpy as cp
CVXPY는 볼록 최적화 문제(Convex Optimization Problem)를 풀어주는 파이썬 라이브러리입니다.
외부 라이브러리이므로, 직접 컴퓨터에 설치해야 합니다.
$ pip install cvxpy
Quadratic Programming
\(\min_{\mathbf{w}}{\mathbf{w}^\mathsf{T}\mathbf{\Sigma w}}\)는 2차 계획법(QP; Quadratic Programming) 문제로 보고 cp.quad_form를 이용해 해결할 수 있습니다.
2차 계획법(QP)는 목적 함수(Objective Function)가 이차식(Convex Quadratic)이고,
제약 함수(Constraint Functions)가 모두 Affine인 볼록 최적화 문제를 말합니다.
General Quadratic Program은 다음과 같은 형태로 표현될 수 있습니다.
\[\min_{x}{\frac{1}{2}x^\mathsf{T} P x+q^\mathsf{T} x}\] \[\text{s.t. }Gx\leq h\] \[Ax=b\]
우리는 분산을 최소화하는 \(\mathbf{w}\)를 찾아야 하므로,
목적 함수는 \(\frac{1}{2}\mathbf{w}^\mathsf{T}\mathbf{\Sigma w}\)이고,
제약 함수는 \(\sum{w_i}=1\), \(w_i\geq 0.05\), \(w_i\leq 0.4\) 3개입니다.
먼저 최소화할 \(\mathbf{w}\)를 변수로 선언합니다.
w = cp.Variable(len(mu))
목적 함수와 제약 함수를 정의합니다.
obj = cp.Minimize(cp.quad_form(w, cov))
constraints = [cp.sum(w) == 1, w >= 0.05, w <= 0.4]
마지막으로 solve()를 이용해 문제를 풀어줍니다.
prob = cp.Problem(obj, constraints)
prob.solve()
w.value를 확인하면 최적화된 가중치가 들어있는 것을 확인할 수 있습니다.
[0.17856414, 0.1656037, 0.4, 0.20583216, 0.05]
삼성전자: 17.9%현대차: 16.6%NAVER: 40.0%POSCO홀딩스: 20.6%LG화학: 5.0%
NAVER와 LG화학뿐만 아니라, 나머지 종목들의 비중도 조금씩 바뀌었습니다.
개별종목 비중 제한을 걸어줌으로써, 전보다 비중이 고르게 분포한 것을 확인할 수 있습니다.
plt.plot(sigma_w, mu_w, zorder=-1)
plt.scatter(
[math.sqrt(cov['005930.KS']['005930.KS']), math.sqrt(cov['005380.KS']['005380.KS']), math.sqrt(cov['035420.KS']['035420.KS']), math.sqrt(cov['005490.KS']['005490.KS']), math.sqrt(cov['051910.KS']['051910.KS'])],
[mu['005930.KS'], mu['005380.KS'], mu['035420.KS'], mu['005490.KS'], mu['051910.KS']])
plt.scatter([sigma_mv5], [mu_mv5])
plt.scatter([prob.value], [np.dot(w.value.T, mu)])
plt.xlabel('risks')
plt.ylabel('returns')
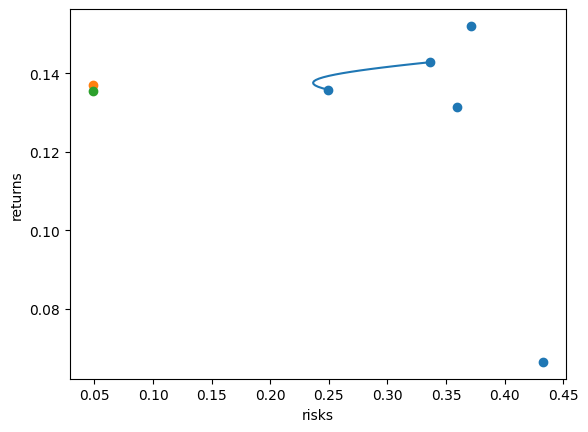
제약조건이 추가되면서 수익률은 살짝 떨어지는 것을 확인할 수 있습니다.
참고: Mean-Variance Optimization - 44살에 배운 미국 금융공학 수업
참고: MPT; 현대포트폴리오 이론