
이 직선... 내 점들이 다 담아질까...? 단순 선형 회귀식 유도와 R 프로그래밍
회귀 분석은 두 변수 사이의 관계를 설명하거나 예측하는 통계적 방법입니다.
회귀분석은 주어진 자료들이 어떤 특정한 경향성을 띠고 있다는 아이디어로부터 비롯됩니다.
선형 회귀 분석은 가장 일반적인 회귀 분석 방법입니다.
선형 회귀 분석은 독립 변수와 종속 변수 사이에 선형 관계가 있다고 가정합니다.
즉, 독립 변수의 변화에 따라 종속 변수가 일정한 비율로 변화한다고 가정합니다.
단순 선형 회귀
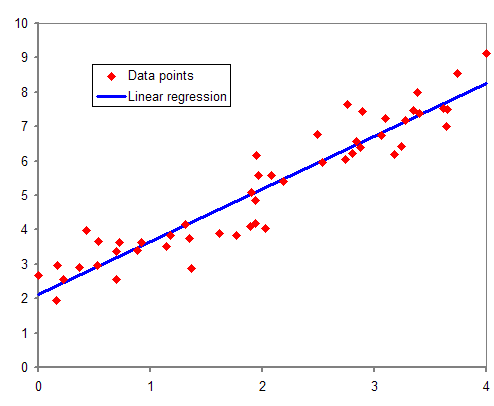
단순 회귀 함수는 독립 변수와 종속 변수 사이의 선형 관계를 나타내는 함수입니다.
단순 회귀 함수는 아래와 같은 형태로 표현됩니다.
\[E(y|x)=\beta_1+\beta_2 x\]\(\beta_1\)과 \(\beta_2\)는 회귀모수(Regression parameter)로, 각각 회귀 함수의 기울기와 절편을 나타냅니다.
기울기 \(\beta_2\)는 아래와 같은 형태로 표현될 수 있습니다.
\[\beta_2=\frac{\Delta E(y|x)}{\Delta x}\]아래는 단순 선형 회귀 모형에 관한 가정입니다.
- \(E(y\mid x)=\beta_1+\beta_2 x\) : \(y\)의 평균값은 선형회귀로 표현 가능
- \(var(y\mid x)=\sigma^2\) : 동일한 분산을 갖는 확률분포
- \(cov(y_i,y_j)=0\) : \(y\)끼리의 선형관계 X
- \(x\)는 확률변수 X, 최소한 2개의 상이한 값을 가짐
- (선택) \(y\sim N[(\beta_1+\beta_2 x),\sigma^2]\)
무작위 오차항
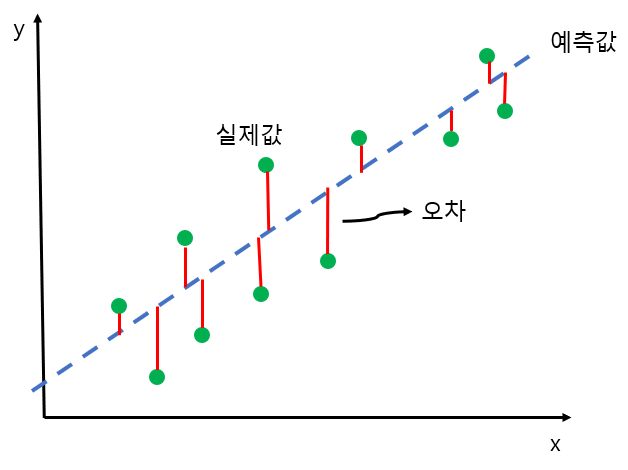
실제 데이터는 완전히 선형적이지 않기 때문에, 무작위 오차항이란 개념을 도입해 식을 변형해야 합니다.
무작위 오차항 \(e\)는 아래와 같이 정의합니다.
\[e=y-E(y|x)=y-\beta_1+\beta_2 x\]이를 \(y\)에 대해서 정리하면 아래와 같이 표현됩니다.
\[y=\beta_1+\beta_2 x+e\]최소 제곱 원칙
\(\beta_1\)과 \(\beta_2\)를 추정하기 위해서는 여러가지 규칙을 적용할 수 있지만, 여기서는 최소 제곱 원칙(Least Squares Principle)을 통해 추정해 볼 것입니다.
우선, 선형 모형을 아래와 같이 정의합니다.
\[\hat{y_i}=b_1+b_2 x_i\]각 점으로부터 선형 모형의 선까지의 수직거리를 최소 제곱 잔차(Least Squares Residuals)이라 합니다.
\[\hat{e_i}=y_i-\hat{y_i}=y_i-b_1-b_2 x_i\]우리가 할 것은 최소 제곱 잔차 \(\hat{e_i}\)가 최소가 되게하는 \(b_1\)과 \(b_2\)를 찾는 것입니다.
\[\min{\sum|\hat{e_i}|}\]거리의 합은 절댓값의 합을 통해 표현할 수 있습니다.
하지만, 식에 절댓값이 포함되면 미분을 통해 최솟값을 구하기 어려워집니다.
그래서 식을 절댓값 대신 제곱을 통해 표현하겠습니다.
\[SSE=\min{\sum\hat{e_i}^2}=\min{\sum(y_i-\hat{y_i})^2}=\min{\sum(y_i-b_1-b_2 x_i)^2}\]식에 절댓값을 취하는 이유는 각 항을 양수로 만들기 위함인데, 제곱을 해도 똑같이 양수로 유지됩니다.
우리가 필요한 것은 \(SSE\)를 최소로 만드는 \(b_1\)과 \(b_2\)이기 때문에, \(b_1\)과 \(b_2\)로 각각 편미분합니다.
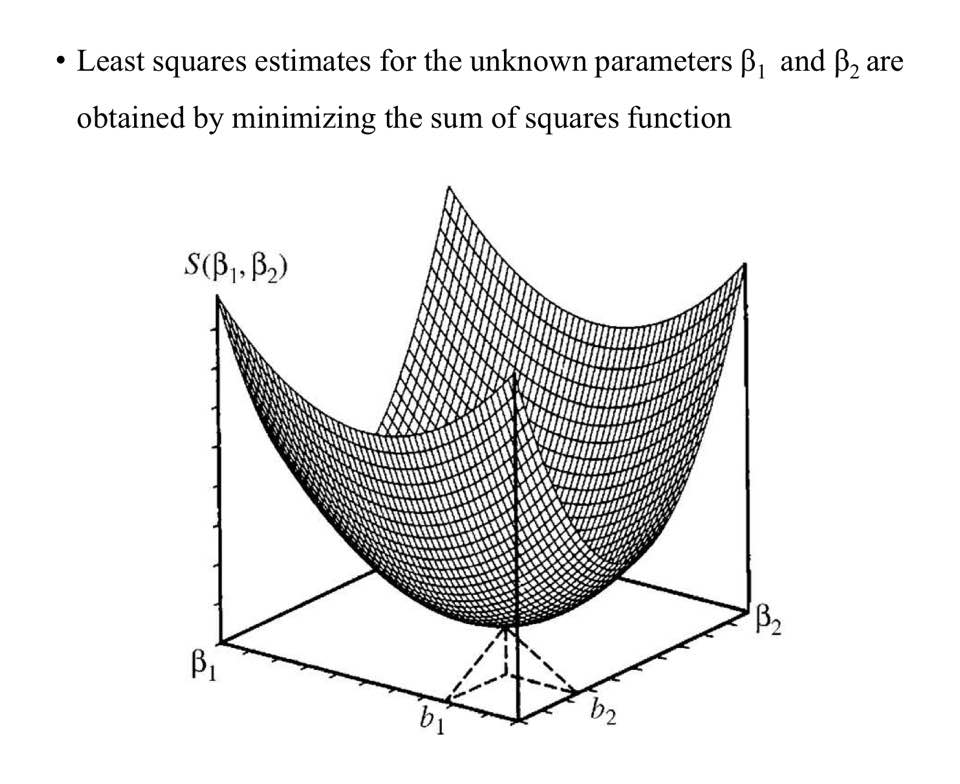
최솟점은 두 식의 값이 0이 되는 지점(기울기가 수평)입니다.
따라서 아래와 같이 표현할 수 있습니다.
\[\sum(y_i-b_1-b_2 x_i)=0\quad\cdots(1)\] \[\sum x_i(y_i-b_1-b_2 x_i)=0\quad\cdots(2)\]여기서 (1) 식을 정리하면 아래와 같습니다.
\[\sum(y_i-b_1-b_2 x_i)=\sum y_i-\sum b_2 x_i-\sum b_1=\sum y_i-b_2\sum x_i-n b_1=0\]\(y\)의 평균 \(\bar{y}\)와 \(x\)의 평균 \(\bar{x}\)는 아래와 동일하기에,
\[\bar{y}=\frac{\sum y_i}{n}\] \[\bar{x}=\frac{\sum x_i}{n}\]\(y\)의 평균이란 \(y_i\)를 다 더해서 \(y_i\)의 개수 \(n\)으로 나눈 것을 의미합니다. \(x\)도 마찬가지입니다.
이를 통해 (1) 식을 다시 정리합니다.
\[\sum(y_i-b_1-b_2 x_i)=\sum y_i-\sum b_2 x_i-n b_1=n\bar{y}-nb_2\bar{x}-n b_1\] \[n\bar{y}-nb_2\bar{x}-n b_1=0\]양변을 \(n\)로 나누어줍니다.
\[\bar{y}-b_2\bar{x}-b_1=0\]\(b_1\)를 우변으로 넘겨줍니다.
\[\bar{y}-b_2\bar{x}=b_1\] \[b_1=\bar{y}-b_2\bar{x}\quad\cdots(3)\](3) 식을 이용해 (2) 식을 정리합니다.
\(b_1\) 자리에 (3) 식을 대입하고,
\[\sum x_i(y_i-b_1-b_2 x_i)=\sum x_i(y_i-(\bar{y}-b_2\bar{x})-b_2 x_i)=\sum x_i(y_i-\bar{y}+b_2\bar{x}-b_2 x_i)=0\]식을 전개합니다.
\[\sum x_i(y_i-\bar{y}+b_2\bar{x}-b_2 x_i)=\sum x_i y_i-\bar{y}\sum x_i+b_2\bar{x}\sum x_i-b_2\sum x_i^2=0\]\(b_2\)로 식을 묶어줍니다.
\[\sum x_i y_i-\bar{y}\sum x_i+b_2\bar{x}\sum x_i-b_2\sum x_i^2=\sum x_i y_i-\bar{y}\sum x_i+b_2(\bar{x}\sum x_i-\sum x_i^2)=0\]\(b_2=(\quad)\) 형태로 식을 변형합니다.
\[b_2=\frac{\sum x_i y_i-\bar{y}\sum x_i}{\sum x_i^2-\bar{x}\sum x_i}=\frac{\sum x_i(y_i-\bar{y})}{\sum x_i(x_i-\bar{x})}\]여기서 한 가지 수학적 트릭을 사용하겠습니다.
- \(\sum x_i(x_i-\bar{x})\)는 \(\sum (x_i-\bar{x})^2\)와 동일합니다.
- \(\sum x_i(y_i-\bar{y})\)도 \(\sum (x_i-\bar{x})(y_i-\bar{y})\)와 동일합니다.
증명
잔차(\(=x_i-\bar{x}\))의 합은 항상 0입니다.
\[\sum(x_i-\bar{x})=\sum x_i-\sum\bar{x}=n\bar{x}-n\bar{x}=0\]\(\sum(x_i-\bar{x})=0\)이면,
\(\bar{x}\sum(x_i-\bar{x})=0\)이고,
\[\sum x_i(x_i-\bar{x})=\sum x_i(x_i-\bar{x})-0=\sum x_i(x_i-\bar{x})-\bar{x}\sum(x_i-\bar{x})\]형태로 표현할 수 있습니다.
식을 정리하면,
\[\sum x_i(x_i-\bar{x})-\bar{x}\sum(x_i-\bar{x})=\sum(x_i(x_i-\bar{x})-\bar{x}(x_i-\bar{x}))=\sum(x_i-\bar{x})(x_i-\bar{x})\] \[\sum x_i(x_i-\bar{x})=\sum (x_i-\bar{x})^2\quad\cdots(4)\]마찬가지로,
\(\sum(y_i-\bar{y})=\sum y_i-\sum\bar{y}=n\bar{y}-n\bar{y}=0\)이기 때문에,
\(\bar{x}\sum(y_i-\bar{y})=0\)이고,
\[\sum x_i(y_i-\bar{y})=\sum(x_i-\bar{x})(y_i-\bar{y})\quad\cdots(5)\]
따라서 \(b_2\)는,
\[b_2=\frac{\sum x_i(y_i-\bar{y})}{\sum x_i(x_i-\bar{x})}=\frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sum(x_i-\bar{x})^2}\quad\cdots(6)\]구한 \(b_2\)를 (3) 식에 대입해 \(b_1\)을 구합니다.
\[b_1=\bar{y}-(\frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sum(x_i-\bar{x})^2})\bar{x}\quad\cdots(7)\]R 프로그래밍
\(\bar{x}\)와 \(\bar{y}\)는 mean 함수를 통해 구할 수 있습니다.
xm <- mean(x)
ym <- mean(y)
이제 \(b_2\)를 계산해 봅시다.
\[b_2=\frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sum(x_i-\bar{x})^2}\]sxy <- sum((x - xm)*(y - ym))
sxx <- sum((x - xm)^2)
b2 <- sxy / sxx
\(b_1\)과 단순 선형 회귀 모델은 아래와 같습니다.
\[b_1=\bar{y}-b_2\bar{x}\]b1 <- ym - b2*xm
b1 + b2*xm
알고리즘 최적화
sxy와 sxx를 구하는 과정은 연산량을 줄이는 방식으로 최적화 될 수 있습니다.
\(\sum\bar{x}y_i=\bar{x}\sum y_i=n\bar{x}\bar{y}\),
\(\sum x_i\bar{y}=\bar{y}\sum x_i=n\bar{x}\bar{y}\),
\(\sum\bar{x}\bar{y}=n\bar{x}\bar{y}\) 이므로,
\[\sum x_i y_i-\sum\bar{x}y_i-\sum x_i\bar{y}+\sum\bar{x}\bar{y}=\sum x_i y_i-n\bar{x}\bar{y}-n\bar{x}\bar{y}+n\bar{x}\bar{y}\]따라서 sxy는,
sxy <- sum(x*y) - n*xm*ym
sxx도 같은 방식으로 구할 수 있습니다.
\(\sum x_i\bar{x}=\bar{x}\sum x_i=n\bar{x}^2\) 이므로,
\[\sum x_i^2-2\sum x_i\bar{x}+\sum \bar{x}^2=\sum x_i^2-2n\bar{x}^2+n\bar{x}^2\]따라서 sxx는,
sxx <- sum(x^2) - n*xm^2
최종적으로 코드를 정리하면 아래와 같습니다.
xm <- mean(x)
ym <- mean(y)
sxy <- sum(x*y) - n*xm*ym
sxx <- sum(x^2) - n*xm^2
b2 <- sxy / sxx
b1 <- ym - b2*xm
b1 + b2*xm