내재 균형 수익률: 시장아, 기대수익률 좀 구해줘
기대수익률은 투자 결정에 중요한 역할을 하는 지표입니다.
투자자들은 기대수익률을 추정하여 투자 대비 얻을 수 있는 수익을 예상하고 투자 포트폴리오를 구성합니다.
기대수익률을 추정하는 방법은 다양하지만, 일반적으로 역사적 수익률을 분석하거나 배당 할인 모형(DDM) 등을 이용해 내재 가치를 계산하고 시장 가치와 비교하는 등을 사용합니다.
하지만 기대수익률은 미래의 불확실성, 정보의 비대칭, 개별 자산의 특성 등의 요인으로 인해 정확하게 예측하기 어렵습니다.

내재 균형 수익률(Implied Equilibrium Return)은 블랙-리터먼 모델(Black-Litterman Model)에서 사용되는 개념으로,
시장 포트폴리오를 최적 포트폴리오로 보고 시장 참여자들이 예상하는 기대수익률을 구한 것입니다.
계산 과정
내재 균형 수익률은 시장이 균형 상태에 있다는 가정에서 시작합니다.
시장 균형 상태란 모든 투자자들이 자신의 위험 선호도에 따라 최적의 포트폴리오를 구성했을 때, 자산의 수요와 공급이 일치하는 상태를 의미합니다.
즉, 현재 시장 포트폴리오가 최적-위험 포트폴리오라고 가정했기 때문에, 역최적화 과정을 통해 내재 균형 수익률을 계산할 수 있습니다.
최적-위험 포트폴리오
이전 포스트에서 포트폴리오의 기대수익률 \(\mu_p\)과 분산 \(\sigma_p^2\)은 각각 \(\mathbf{w}^\mathsf{T}E(r)\)와 \(\mathbf{w}^\mathsf{T}\mathbf{\Sigma w}\)가 됨을 확인했습니다.
최적-위험 포트폴리오는 기대수익률은 커지고 위험은 작아지도록 하는 \(\mathbf{w}\)를 찾습니다.
\[\max_{\mathbf{w}}{\mathbf{w}^\mathsf{T}E(r)-\frac{\lambda}{2}\mathbf{w}^\mathsf{T}\mathbf{\Sigma w}}\]\(\mathbf{w}^\mathsf{T}\mathbf{\Sigma w}\)를 \(\mathbf{w}\)로 미분하면 \(2\mathbf{\Sigma w}\)가 되기 때문에 계수 2를 지우기 위해 \(\frac{1}{2}\)을 곱한 형태를 사용합니다.
여기서 \(\lambda\)는 투자자의 위험 회피성향(Risk aversion)을 나타냅니다.
최적-위험 포트폴리오를 구할 때는 위 식을 그대로 계산해 \(\mathbf{w}\)를 구하면 되지만,
내재 균형 수익률을 구할 때는 \(\mathbf{w}\)(시가총액)을 이미 알고 있는 상태에서 \(E(r)\)을 역산해야 합니다.
역최적화
기울기가 0이 되는 지점에서 \(\mathbf{w}^\mathsf{T}E(r)-\frac{\lambda}{2}\mathbf{w}^\mathsf{T}\mathbf{\Sigma w}\)는 최대가 됩니다.
\[\frac{\partial}{\partial\mathbf{w}}(\mathbf{w}^\mathsf{T}E(r)-\frac{\lambda}{2}\mathbf{w}^\mathsf{T}\mathbf{\Sigma w})=0\] \[E(r)-\lambda\mathbf{\Sigma w}=0\] \[E(r)=\lambda\mathbf{\Sigma w}\]이렇게 시장의 \(\mathbf{w}\)로부터 구한 \(E(r)\)을 내재 균형 수익률 \(\Pi\)라고 합니다.
\[\Pi=\lambda\mathbf{\Sigma w}\quad\cdots(1)\]위험 회피성향
위험 회피성향은 위험 한 단위당 투자자가 요구하는 초과수익률을 의미합니다.
일반적으로 1.1~1.7 사이의 상수를 설정하며, 아래 식을 통해 계산할 수 있습니다.
\[\lambda=\frac{E(r_m)-r_f}{\sigma_m^2}\quad\cdots(2)\]위험 회피성향은 블랙-리터만 모형에서 내재 균형 수익률에 대한 Scaling Factor 역할을 합니다.
실습
내재 균형 수익률을 계산하기 위해서는 시장 전체 종목에 대해 \(\mathbf{w}\)를 구해야 하지만,
실습에서는 시장이 아래 5개의 종목으로만 구성되어 있다고 가정하고 실습을 진행했습니다.
SK하이닉스, 현대차, NAVER, POSCO홀딩스, LG화학 다섯 개 종목의 주가 데이터를 다운로드합니다.
import yfinance as yf
tickers = ['000660.KS', '005380.KS', '035420.KS', '005490.KS', '051910.KS']
df = yf.download(tickers, start='2019-01-01')
prices = df["Adj Close"].dropna(how="all")
returns = prices.pct_change().dropna(how="all")
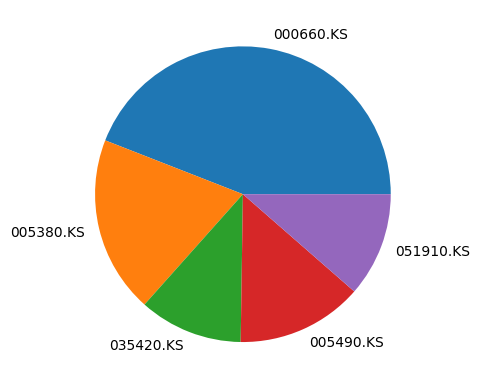
시가총액을 통해 \(\mathbf{w}\)를 계산합니다.
outstanding_shares = {
'000660.KS': 728002365,
'005380.KS': 211531506,
'035420.KS': 162408594,
'005490.KS': 84571230,
'051910.KS': 70592343,
}
market_caps = { ticker: (prices[ticker][-1] * shares) for ticker, shares in outstanding_shares.items() }
import matplotlib.pyplot as plt
plt.pie(market_caps.values(), labels=market_caps.keys())
plt.show()
import pandas as pd
total_market_cap = sum(market_caps.values())
market_weights = pd.Series(market_caps.values(), index=market_caps.keys()).sort_index() / total_market_cap
위험 회피성향 \(\lambda\)를 계산하기 위해 KOSPI(시장) 주가 데이터를 다운로드합니다.
market_prices = yf.download('^KS11', start='2019-01-01')["Adj Close"].dropna(how="all")
market_returns = market_prices.pct_change().dropna(how="all")
(2)식을 이용해 위험 회피성향을 계산합니다.
무위험 수익률 \(r_f\)는 최근 KOFR 금리인 3.2%로 설정했습니다.
market_expected_return = market_returns.mean() * 252
market_variance = market_returns.var() * 252
risk_free_rate = 0.032
lambd = (market_expected_return - risk_free_rate) / market_variance
1.13373
구한 \(\lambda\)와 (1)식을 이용해 내재 균형 수익률 \(\Pi\)를 계산합니다.
\[\Pi=\lambda\mathbf{\Sigma w}\quad\cdots(1)\]covariances = returns.cov() * 252
implied_returns = lambd * covariances @ market_weights
Ticker
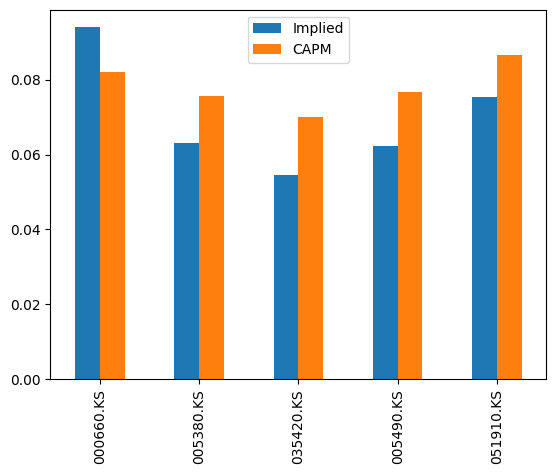
000660.KS 0.093971
005380.KS 0.063106
005490.KS 0.062316
035420.KS 0.054429
051910.KS 0.075419
dtype: float64
즉, 시장 참여자들이 예상하는 각 종목의 기대수익률은 아래와 같습니다.
SK하이닉스: 9.4%현대차: 6.3%NAVER: 6.2%POSCO홀딩스: 5.4%LG화학: 7.5%
CAPM 기대수익률
각 종목의 베타는 아래와 같이 구합니다.
\[\beta_i=\frac{Cov(r_m, r_i)}{Var(r_m)}\]import numpy as np
betas = pd.Series([(np.cov(returns[ticker], market_returns)[0, 1] * 252) for ticker in tickers], index=tickers) / market_variance
000660.KS 1.227264
005380.KS 1.072311
035420.KS 0.931907
005490.KS 1.097943
051910.KS 1.342018
dtype: float64
네이버증권에서 제공하는 52주 베타는 일일 수익률이 아닌, 주간 수익률 기준 베타입니다.
CAPM 공식은 아래와 같습니다.
\[E(r_i)=r_f+\beta_i(E(r_m)-r_f)\]expected_returns = risk_free_rate + betas * (market_expected_return - risk_free_rate)
000660.KS 0.081939
005380.KS 0.075634
035420.KS 0.069921
005490.KS 0.076677
051910.KS 0.086609
dtype: float64
CAPM을 통해 계산한 각 종목의 기대수익률은 아래와 같습니다.
SK하이닉스: 8.2%현대차: 7.6%NAVER: 7.0%POSCO홀딩스: 7.7%LG화학: 8.7%
내재 균형 수익률과 비교하면 아래와 같습니다.
df = pd.DataFrame({'Implied': implied_returns, 'CAPM': expected_returns}, index=expected_returns.index)
df.plot.bar()